论文原稿： Neural network for topology optimization.

http://arxiv.org/abs/1709.09578http://arxiv.org/abs/1709.09578摘要部分：本文针对传统拓扑结构优化的材料分布问题，采取了图像分割的思路，利用深度学习方法的强大功能作为高效的像素级图像标记技术来执行拓扑优化。介绍了卷积编码器-解码器。进行的实验证明了能够加速优化过程。提出的方法具有泛化特性。

本手法关键特征：1.加速优化进程 ；2.优秀的泛化特性；3.发展前景良好。

在研究机械结构拓扑优化时，会考虑一个设计域，一般给它赋予线性各向同性材料的属性，并且进行方形有限元离散化。材料分布由二进制密度变量定义，设计域材料不存在（void）即为0，存在即1. 这个问题用数学公式可以表示为：

c是挠度，是元素的位移向量，是具有单位杨氏模量的单元的单元刚度矩阵。U和F分别为全局位移和力矢量，K是全局刚度矩阵。 V(x)和V分别是材料体积和设计域体积，f_0是规定的体积分数。在解决材料分布问题时，具有离散性质，可以是实体，可以是空白。在处理时采用二进制变量替换连续变量，,j=0,1,2...N.? 最普遍的方法叫做SIMP法，是一种基于梯度迭代的带惩罚值的非二元解方法。PS：SIMP法请参考其他文献，包括SIMP在matlab，python中的使用，之后我会阅读。

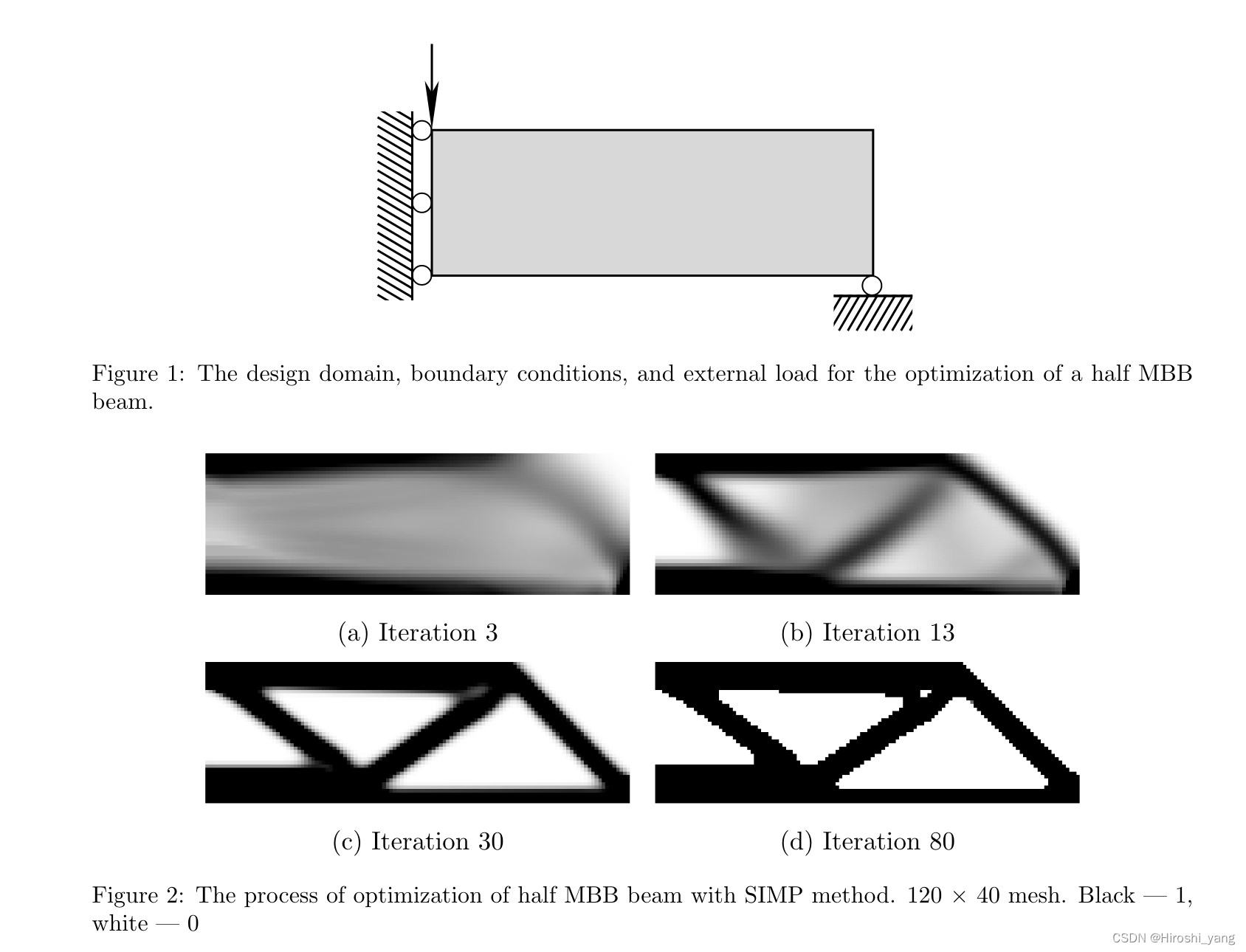
采用的MBB梁的结构优化迭代情况如图所示，边界条件，加载等不做赘述。在初始迭代时，对设计域内的材料进行一半重新分配。优化过程的其余部分包括像素的过滤：具有中间值的密度收敛到二进制值，并且获得的结构的轮廓几乎保持不变。

在上一节中，获得的图像可以被解释为最终结构的模糊图像（其他因素扭曲的图像）。只有两种类型物体的结构为图像，不包含中间值，因此可以解释为图像的mask（掩膜）。所以，优化从的过程模拟了两类图像分割或者前景-背景的分割过程。

所以提出了拓扑优化流程：使用SIMP法执行初始迭代并获得非二进制密度的分布；使用神经网络对获得的图像进行分割并将分布收敛到{0，1}解。

这里我们介绍拓扑优化神经网络，这是一个深度全卷积神经网络旨在在拓扑优化过程中执行密度收敛。

模型输入与输出

输入是两个灰度图像（或一个双通道图像）：第一个是设计域内的密度分布（获得于拓扑优化求解器的最后一次迭代）。第二个是最后一次更新的密度的梯度(第n代与第n-1代密度之差)；模型输出是与输入分辨率相同的灰度图，代表着预测的最终结构。

结构解析

该结构模拟图像分割沙漏形状的常见结构。所提出的模型具有编码器网络和相应的解码器网络，然后是最终的逐像素分类层。如图所示

这个编码器包括6个卷积层，每一层有3*3的卷积核，跟着后面是ReLU非线性。前两层有16个卷积核，该块后面是大小为2*2的窗口中的最大元素的池化。接下来的两层有32个内核，后面是MaxPooling层，最后一块是由两层组，每层有64个内核。解码器的网络则是与之对称的反过来。但是MaxPooling层需要替换为Upsampling层，然后与U-Net中执行相应的低级层之间的串联（skip connection）。池化操作将后续网络的不变性引入到输入的小平移中。来自不同层的skip connections 允许同时利用原始低级表示和高级编码表示，解码器后面是具有一个内核和sigmoid激活函数的卷积层。使用2个dropout层来作为我们网络的正则化。输入的高度和宽度可以变化，但是它们必须能被4整除，以保证计算图中张量形状的一致性。本网络结构有192,113个参数

为了训练上述模型，我们需要系统1的示例解决方案。数据集来自于使用Topy生成的合成数据（一种基于SIMP法的2D和3D拓扑优化开源求解器），针对数据库，我们对伪随机问题进行了采样，并执行了100次标准SIMP法迭代。每个问题都由约束和负载定义，选择的样本：1.按照泊松分布取固定x和y平移的节点数量以及负载数量：；选择边界节点概率是内部节点的100倍。负载值为-1；体积分数按照正态分布。

获取的有10,000个对象，每一个都是形状为100*40*40的张量：在常规40*40的网格上定义的问题的优化过程的100次迭代。

我们使用上一节提取的数据来训练模型。在第k次迭代后我们停止用SIMP求解器，并且使用获得的设计变量作为模型的输入。输入图像通过D4组的变换进行了增强：水平和垂直翻转以及90度旋转。k是从某个特定分布中采样所得。让我们感兴趣的泊松分布以及离散均匀分布U[1,100]。为了训练网络我们使用下面的目标函数：

其中置信度损失（L_conf）是二元交叉熵：

其中N*M是图像的分辨率。上面的L_vol代表体积分数的约束：

使用默认参数的ADAM优化器，在训练过程中将学习率减半一次，代码：python2；后端：keras和tensorflow；NVIDIA Tesla K80.从头开始训练化了80～90分钟。

我们在获得结构的准确性和平均的时间消耗上面将我们的方法与标准SIMP法进行了比较。我们使用两个常见的图像分割评估指标：二进制精度和交并集（IoU）。设为类像素总数，是预测属于p类的t类像素总数。所以

我们测试了四个具有相同结构但是使用不同设定进行训练的神经网络，我们通过停止SIMP法训练后的迭代次数是从不同的分布中采样的。我们通过选择离散均匀分布U[1,100]来训练一个网络，另外三个则使用泊松分布训练，.（即选择在第多少代停止SIMP法）

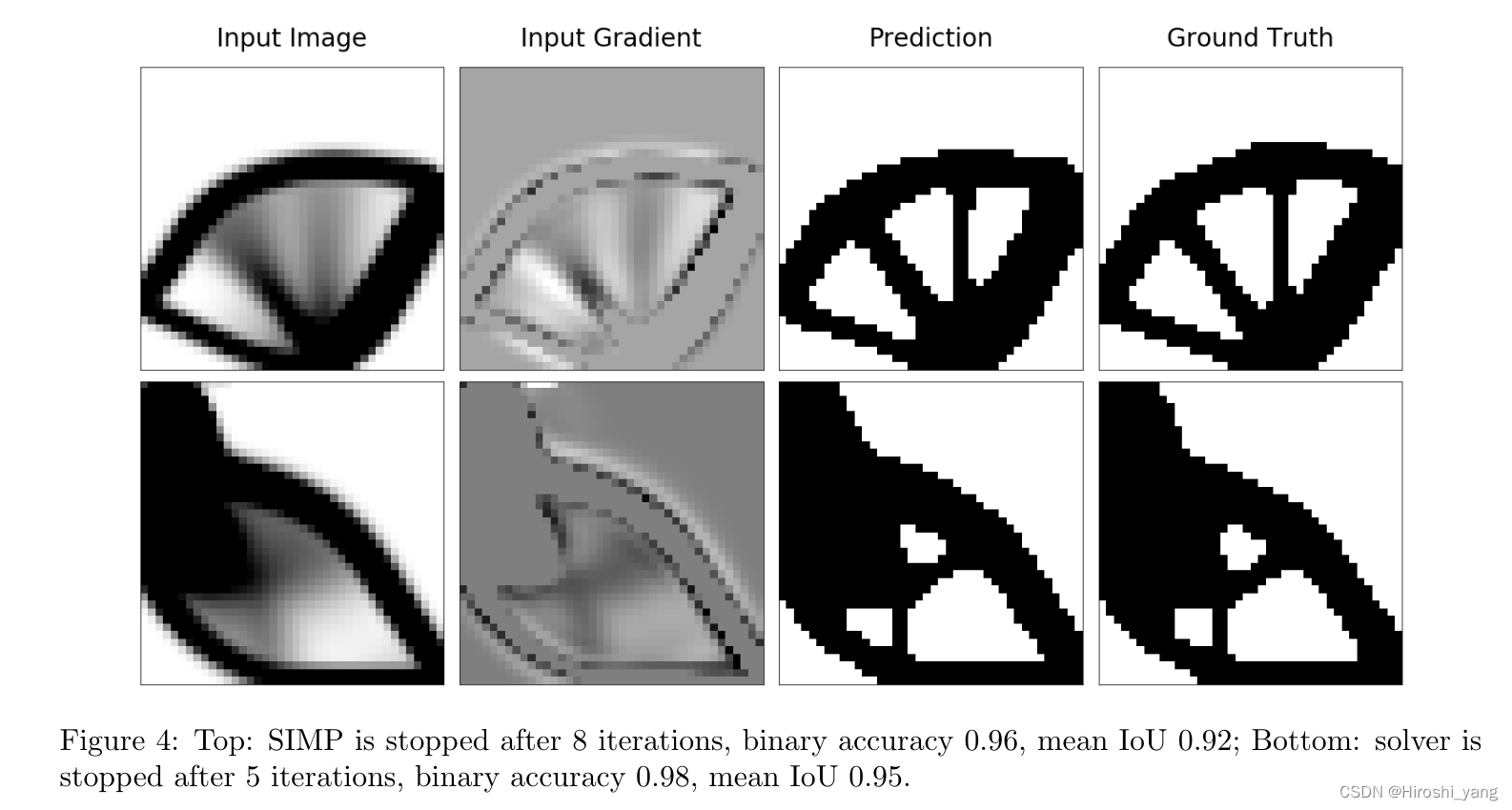
上图展示了我们的节后在迭代5次之后也能恢复为最终的结构，该模型的输出与SIMP算法的输出结构，结构的整体拓扑是相同的。此外，所提出的方法消耗的时间几乎减少了20倍。使用不同策略训练的神经网络产生接近的结果：模型保留最终结构直至一些罕见的像素级变化。然而，这次模型的准确性取决于SIMP算法执行的初始迭代次数。下表总结了一系列的实验结果，与SIMP法相同次数迭代后应用的阈值相比，经过训练的模型表现出足够准确的结果。有些模型在迭代5～10次后会受益而另一些需要在中间或者结束时表现出更好的结果。所提出的流程可以显著加速整体算法，同时将精度最小化，尤其是在优化过程开始时使用CNN。

另外，为了证明方法的泛化性，我们还生成在40*40的规则网格上定义的热传导问题的小数据集。问题的精确解和中间密度的获取方式和前面的例子完全一样。

根据结果发现，在优化的初始阶段，预训练CNN的结果比阈值化的结果更加准确，当数据集的训练和验证数据集来自同一分布时，我们的模型能够精准地近似映射到最终结构。即使将CNN应用于其他数据集，也会在最开始迭代期间就模仿SIMP的方法的更新，所有我们的方法可以快速预测各种拓扑优化问题。

---

我们训练的模型是基于40*40尺寸的图像进行的，我们还可视化了应用到不同分辨率时的问题的结果。可以得出，纵横比的变化以及输入数据分辨率的合理变化不会影响模型的精度，能够成功构建最终的结构。输入的数据的大小的变化需要对模型进行额外的训练，因为常见的典型大小随着图像分辨率的增加而变化。演示案例不需要调整神经网络，并且允许将一种分辨率转移到另一种分辨率。

这篇文章提出的方式很适合设计工学，想要利用深度学习进行结构优化研究学习的学生学习，先总结以上内容在此，主要是自己学习总结而用，关于代码的复建和深入学习就是之后需要研究的了。希望各位有所收获。

上一篇：[源码解析] PyTorch分布式优化器(2)----数据并行优化器_1

下一篇：2023年NBA全明星赛