教学优化算法（Teaching-learning-based optimization, TLBO）是一种基于种群的启发式随机群智能算法。与其他的进化算法类似，该方法也存在迭代过程。该过程分为两步，每个阶段执行各自的优化。相比于其他的算法，教学优化算法的主要优势在于概念简单、超参数量少、收敛快速。本文对教学优化算法进行简单介绍，并对教学优化算法在各方面的一些改进扩展进行描述。

• 近年来，随着各种领域的优化问题不断增多，更多的优化方法被提出以适用于各类问题。在早期，大多数优化算法主要关注数学技术。而这些方法的主要问题在于容易陷入局部最优解而无法找到最优解。而最近，各种启发式算法成为了热点[1]，这其中包括如遗传算法、演化规划、演化策略、遗传规划等所属的进化算法，蚁群算法、粒子群算法等所属的群智能算法，以及引力搜索算法、人工水滴算法等所属的非生物学元启发式算法。
• 然而这些方法中，除了种群大小和迭代次数，往往还存在一些其他需要设定的超参数。合理设置和适当调整这些特定于算法的超参数，对于这些算法的搜索能力至关重要。因此，希望能开发没有算法特定超参数的优化算法。
• Rao等人提出了基于教学学习的优化算法[2-3]，它的灵感来自于课堂教学过程，模仿教师对学生的影响。与其他群体智能算法类似，教学优化算法基于种群的启发式随机优化算法，但它的优点在于不需要任何特定于算法的超参数。

在教学优化算法中，学生被当作是分布在决策变量空间中的搜索点，其中，最优的学生被定义为该班级的教师。与传统的进化算法和群智能算法不同的是教学优化算法的迭代进化过程包括教学阶段和学习阶段，如图1所示。在教学阶段，为了提高班级的平均水平，学生会通过向教师学习来提高自身水平；之后在学习阶段，会通过与随机选择的另一位学生进行互动学习来提高自身水平。

记决策变量维度为$D$，第$i$个学生（搜索点）表示为$X_i=(x_{i1},x_{i2},\dots ,x_{iD})$，$f(X_i)$表示为适应度函数，目标是尽可能接近该函数的极小值。$N$表示学生总量。班级中第$i$个学生$X_i=(x_{i1},x_{i2},\dots ,x_{iD})$可以被初始化为：

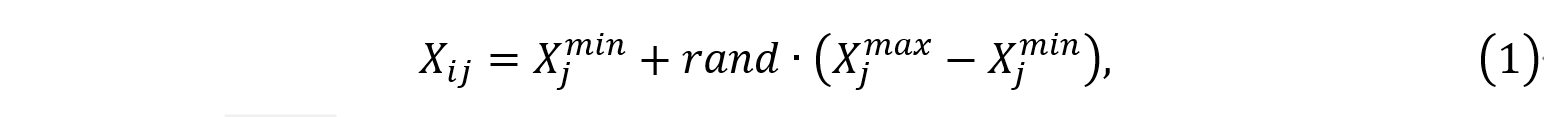
其中$X_j^{max}$和$X_j^{min}$分别为第j维决策变量的上下界，rand是[0,1]之间的随机数。

在教学阶段，模拟学生通过学习教师与班级平均水平的差异来提高自身水平。对于班级中的第i个学习者$X_i$，更新机制表示如下：

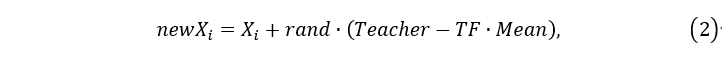
其中，$new{X}_i$是学生$X_i$的新取值，$Teacher$是当前最优值的学生，并且$Mean=1/N{\sum }_{i=1}^N{X}_i$是班级的平均状态。$TF=round[1+rand(0,1)]$是一个教学因子，决定了要改变的均值的大小。$rand$是随机向量，其每个元素都是$[0,1]$范围内的随机数。在教学阶段之后，学生的值将采用其原先适应度和新适应度之间较小的，然后进入学习阶段。

在学习阶段，模拟学生之间相互讨论、展示和交流的方式进行学习，以提高自身水平。对于学习者$X_i$，更新公式为：

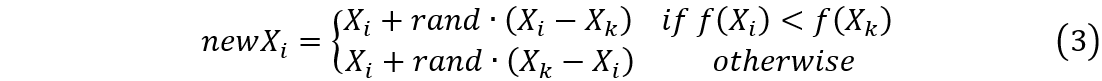
其中，$new{X}_i$是学生$X_i$的新取值，$X_k$是从班级中随机选取的另一个与$X_i$不同的学生，$f(X_i)$和$f(X_k)$分别是学生$X_i$和$X_k$的适应度。$rand$是随机向量，其每个元素都是$[0,1$]范围内的随机数。和教学阶段类似，学生的值将采用其原先适应度和新适应度之间较小的，然后进入下一轮的教学阶段。

整个算法流程总结如下：

• 输入：初始化$N$（学生数量）和$D$（决策变量维度）
• 输出：教师$X_{Teacher}$
• Step1 初始化所有的学生，并评估适应度函数值。
• Step2 令适应度函数值最小的学生为$X_{Teacher}$，计算所有学生的均值$X_{Mean}$.
• Step3 当满足终止条件（通常为最大轮次）时，直接退出，输出结果;否则继续向下执行。
• Step4 对于每一个学生，首先计算$TF=round(1+rand(0,1))$;再根据公式（2）计算学生的新适应度函数值；如果新适应度函数值低于原适应度函数值，则更新学生的值。
• Step5 对于每一个学生，随机选取另一个与之不同的学生，用公式（3）计算学生的新适应度；如果新适应度函数值低于原适应度函数值，则更新学生的值。
• Step6 更新$X_{Teacher}$和$X_{Mean}$，重复执行Step3.
  注意，上述过程中没有考虑到有约束的情况。对于有约束问题，可以采用多种类型的约束处理技术，例如静态罚函数、动态罚函数、自适应罚函数等，也有一些文献[4-5]对教学优化问题进行改进，使其适用于各种有约束问题。

1. 教学优化算法属于全局优化算法，与遗传算法和粒子群算法类似，在整个解空间进行搜索，可以达到全局最优值。而且相比于粒子群算法，教学优化算法简化了每一轮内的信息共享机制，所有进化的个体可以更快收敛到全局最优解。
2. 学习阶段具有并行性，各个学生之间的学习是一种随机的并行关系，加快了全局搜索的速度。
3. 算法简易，超参数少，相比于遗传算法和粒子群算法，教学优化算法所需要的超参数只有种群数量，不涉及到优化过程本身。从而简化了优化的初始设置过程。

1. 记忆能力较差。最初的解集在搜索过程中将会改变，不能很好地保持种群多样性。
2. 教学优化算法的理论基础薄弱。对于其中存在的如多样性过早丢失之类的缺点，缺乏理论的验证。
3. 缺少收敛分析方法，同属于全局优化算法的遗传算法和粒子群算法都有比较成熟的方法判定收敛，而教学优化算法很难准确估计收敛速度[6]。
4. 在教学阶段具有固有的原点偏差，也即该算法有向原点附近搜索的倾向性。当解决一些远离原点的优化问题时，该算法通常会失去优势。有些文献基于这一点对教学优化算法进行改进[8]。

教学优化算法的改进和变种非常多，下面介绍一些常用改进方案。
在最初的教学优化算法中，只有一个教师进行教学，当学生的适应度函数值普遍较高时，教学阶段所带来的效果不够明显；而当学生的适应度函数值普遍较低时，收敛速度又会降低。所以改进的教学优化算法提高了教师的教学能力，通过改进，根据学生的适应度函数值高低将班级划分为多个小班级，每个小班级选取一名教师进行该小班级的教学。进一步，这种多个小班级，可以采用K均值聚类的方式实现。
此外，最初的教学优化算法中教学因子只能是1或2，能力过分单一，影响搜索的能力，容易走入极端的学习状态。所以改进了其中的教学因子部分，使其变为一个自适应的连续值，其表达式为$TF=T{F}_{max}?\frac{T{F}_{max}?T{F}_{min}}{ite{r}_{max}}iter$，其中$T{F}_{max}$和$T{F}_{min}$分别为$TF$的最大值和最小值，$ite{r}_{max}$为最大迭代次数。这种方式与粒子群算法中的线性递减惯性权重[7]类似，能在搜索初期加快迭代的步伐，而在后期进行稳定的搜索。
如果采用小班级教学时，在学习阶段，由于每个小班级中的成员与其他成员相似度可能会比较高，所以可以考虑采用和其他班级成员进行交互学习，提升学习阶段的效果。这种方法还能在一定程度上避免算法陷入局部极小值，保存了样本多样性。

本文对教学优化算法进行介绍，并通过三种函数样例测试该算法的优化效果。教学优化算法由于其自身简单、易收敛的优势，在应用领域经常会被用到。不过该算法在一些场景下仍然存在不足，研究人员基于这些问题也开发出许多不同的变体，以提高其优化性能，并已成功应用于各种优化领域。除此之外，对教学优化算法的收敛特性和动力学进行理论分析仍然是十分有必要的。

[1] Luke S. Essentials of Metaheuristics. Lulu, 2013[J].
[2] Rao R V, Savsani V J, Vakharia D P. Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43(3): 303-315.
[3] Rao R V, Savsani V J, Vakharia D P. Teaching–learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information sciences, 2012, 183(1): 1-15.
[4] Yu K, Wang X, Wang Z. Constrained optimization based on improved teaching–learning-based optimization algorithm[J]. Information Sciences, 2016, 352: 61-78.
[5] Rao R V, Savsani V J, Balic J. Teaching–learning-based optimization algorithm for unconstrained and constrained real-parameter optimization problems[J]. Engineering Optimization, 2012, 44(12): 1447-1462.
[6] 黄祥东. 教与学优化算法的研究与应用[D].中国矿业大学,2016.
[7] Shi Y, Eberhart R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406). IEEE, 1999, 3: 1945-1950.
[8] 平良川,孙自强.教学优化算法的改进及应用[J].计算机工程与设计,2018,39(11):3531-3537.

上一篇：超10万家火锅餐饮商家开启抖音经营，用好数字化营销破局出圈

下一篇：系统优化_3